Matemática
Origem: Wikipédia, a enciclopédia livre.
A matemática (do grego μάθημα, transl. máthēma, "ciência"/"conhecimento"/"aprendizagem"; e μαθηματικός, transl. mathēmatikós, "apreciador do conhecimento") é a ciência do raciocínio lógico e abstrato. A Matemática estuda quantidades, medidas, espaços, estruturas e variações. Um trabalho matemático consiste em procurar por padrões, formular conjecturas e, por meio de deduções rigorosas a partir de axiomas e definições, estabelecer novos resultados.
A Matemática vem sendo construída ao longo de muitos anos. Resultados e teorias milenares se mantêm válidos e úteis e ainda assim a matemática continua a desenvolver-se permanentemente.
Registros arqueológicos mostram que a matemática sempre foi parte da atividade humana. Ela evoluiu a partir de contagens, medições, cálculos e do estudo sistemático de formas geométricas e movimentos de objetos físicos. Raciocínios mais abstratos que envolvem argumentação lógica surgiram com os matemáticos gregos aproximadamente em 300 a.C., notadamente com a obra "Os Elementos" de Euclides. A necessidade de maior rigor foi percebida e estabelecida por volta do século XIX.
A Matemática se desenvolveu principalmente na Mesopotâmia, no Egito, na Grécia, na Índia, no Oriente Médio. A partir da Renascença o desenvolvimento da Matemática intensificou-se na Europa, quando novas descobertas científicas levaram a um crescimento acelerado que dura até os dias de hoje.
Há muito tempo busca-se um consenso quanto à definição do que é a matemática. No entanto, nas últimas décadas do século XX tomou forma uma definição que tem ampla aceitação entre os matemáticos: matemática é a ciência das regularidades (padrões). Segundo esta definição, o trabalho do matemático consiste em examinar padrões abstratos, tanto reais como imaginários, visuais ou mentais. Ou seja, os matemáticos procuram regularidades nos números, no espaço, na ciência e na imaginação e formulam teorias com as quais tentam explicar as relações observadas. Uma outra definição seria que matemática é a investigação de estruturas abstratas definidas axiomaticamente, usando a lógica formal como estrutura comum. As estruturas específicas geralmente têm sua origem nas ciências naturais, mais comumente na física, mas os matemáticos também definem e investigam estruturas por razões puramente internas à matemática (matemática pura), por exemplo, ao perceberem que as estruturas fornecem uma generalização unificante de vários subcampos ou uma ferramenta útil em cálculos comuns.
A Matemática é usada como uma ferramenta essencial em muitas áreas do conhecimento, tais como engenharia, medicina, física, química, biologia, e ciências sociais. Matemática Aplicada, ramo da matemática que se ocupa de aplicações do conhecimento matemático em outras áreas do conhecimento, às vezes leva ao desenvolvimento de um novo ramo, como aconteceu com Estatística ou Teoria dos jogos. O estudo de Matemática pura, ou seja, da matemática pela matemática, sem a preocupação com sua aplicabilidade, muitas vezes mostrou-se útil anos ou séculos adiante, como aconteceu com os estudos das cônicas ou de Teoria dos números feitos pelos gregos, úteis, respectivamente, em descobertas sobre astronomia feitas por Kepler no século XVII, ou para o desenvolvimento de segurança em computadores nos dias de hoje.
Índice[esconder] |
[editar] História
O primeiro objeto conhecido que atesta a habilidade de cálculo é o osso de Ishango, uma fíbula de babuíno com riscos que indicam uma contagem, que data de 20 000 anos atrás.[1]
Muitos sistemas de numeração existiram. O Papiro de Rhind é um documento que resistiu ao tempo e mostra os numerais escritos no Antigo Egito.
O desenvolvimento da matemática permeou as primeiras civilizações, e tornou possível o desenvolvimento de aplicações concretas: o comércio, o manejo de plantações, a medição de terra, a previsão de eventos astronômicos, e por vezes, a realização de rituais religiosos.
A matemática começou a ser desenvolvida motivada pelo comércio, medições de terras para a agricultura, registro do tempo, astronomia. A partir de 3000 a.C., quando Babilônios e Egípcios começaram a usar aritmética e geometria em construções, astronomia e alguns cálculos financeiros, a matemática começou a se tornar um pouco mais sofisticada. O estudo de estruturas matemáticas começou com a aritmética dos números naturais, seguiu com a extração de raízes quadradas e cúbicas, resolução de algumas equações polinomiais de grau 2, trigonometria, frações, entre outros tópicos.
Tais desenvolvimentos são creditados às civilizações acadiana, babilônica, egípcia, chinesa, ou ainda, àquelas do vale dos hindus. Por volta de 600 a.C., na civilização grega, a matemática, influenciada por trabalhos anteriores e pela filosofia, tornou-se mais abstrata. Dois ramos se distinguiram: a aritmética e a geometria. Formalizaram-se as generalizações, por meio de definições axiomáticas dos objetos de estudo, e as demonstrações. A obra Os Elementos de Euclides é um registro importante do conhecimento matemático na Grécia do século III a.C.
A civilização muçulmana permitiu que a herança grega fosse conservada, e propiciou seu confronto com as descobertas chinesas e hindus, notadamente na questão da representação numérica [carece de fontes]. Os trabalhos matemáticos desenvolveram-se consideravelmente tanto na trigonometria, com a introdução das funções trigonométricas, quanto na aritmética. Desenvolveu-se ainda a análise combinatória, a análise numérica e a álgebra de polinômios.
Na época do Renascentismo, uma parte dos textos árabes foi estudada e traduzida para o latim. A pesquisa matemática se concentrou então na Europa. O cálculo algébrico desenvolveu-se rapidamente com os trabalhos dos franceses François Viète e René Descartes. Nessa época também foram criadas as tabelas de logaritmos, que foi extremamente importante para o avanço científico dos séculos XVI a XX, sendo substituídas apenas após a criação de computadores. A percepção de que os números reais não são suficientes para resolução de certas equações também data do século XVI. Já nessa época começou o desenvolvimento dos chamados números complexos, apenas com uma definição e quatro operações. Uma compreensão mais profunda dos números complexos só foi conquistada no século XVIII com Euler.
No início do século XVII, Isaac Newton e Leibniz descobriram a noção de cálculo infinitesimal e introduziram a noção de fluxor (vocábulo abandonado posteriormente). Ao longo dos séculos XVIII e XIX, a matemática se desenvolveu fortemente com a introdução de novas estruturas abstratas, notadamente os grupos (graças aos trabalhos de Évariste Galois) sobre a resolubilidade de equações polinomiais, e os anéis definidos nos trabalhos de Richard Dedekind.
O rigor em Matemática variou ao longo do tempo: os gregos antigos foram bastante rigorosos em suas argumentações; já no tempo da criação do Cálculo Diferencial e Integral, como as definições envolviam a noção de limite que, pelo conhecimento da época, só poderia ser tratada intuitivamente, o rigor foi menos intenso e muitos resultados eram estabelecidos com base na intuição. Isso levou a contradições e "falsos teoremas". Com isso, por volta do século XIX, alguns matemáticos, tais como Bolzano, Karl Weierstrass e Cauchy dedicaram-se a criar definições e demonstrações mais rigorosas.
A Matemática ainda continua a se desenvolver intensamente por todo o mundo nos dias de hoje. [carece de fontes]
[editar] Áreas e metodologia
As regras que governam as operações aritméticas são as da álgebra elementar e as propriedades mais profundas dos números inteiros são estudadas na teoria dos números. A investigação de métodos para resolver equações leva ao campo da álgebra abstrata, que, entre outras coisas, estuda anéis e corpos — estruturas que generalizam as propriedades possuídas pelos números. O conceito de vetor, importante para a física, é generalizado no espaço vetorial e estudado na álgebra linear, pertencendo aos dois ramos da estrutura e do espaço.
O ensino da geometria.
Entender e descrever as alterações em quantidades mensuráveis é o tema comum das ciências naturais e o cálculo foi desenvolvido como a ferramenta mais útil para fazer isto. A descrição da variação de valor de uma grandeza é obtida por meio do conceito de função. O campo das equações diferenciais fornece métodos para resolver problemas que envolvem relações entre uma grandeza e suas variações. Os números reais são usados para representar as quantidades contínuas e o estudo detalhado das suas propriedades e das propriedades de suas funções consiste na análise real, a qual foi generalizada para análise complexa, abrangendo os números complexos. A análise funcional trata de funções definidas em espaços de dimensões tipicamente infinitas, constituindo a base para a formulação da mecânica quântica, entre muitas outras coisas.
Para esclarecer e investigar os fundamentos da matemática, foram desenvolvidos os campos da teoria dos conjuntos, lógica matemática e teoria dos modelos.
Quando os computadores foram concebidos, várias questões teóricas levaram à elaboração das teorias da computabilidade, complexidade computacional, informação e informação algorítmica, as quais são investigadas na ciência da computação
Uma teoria importante desenvolvida pelo ganhador do Prémio Nobel, John Nash, é a teoria dos jogos, que possui atualmente aplicações nos mais diversos campos, como no estudo de disputas comerciais.
Os computadores também contribuíram para o desenvolvimento da teoria do caos, que trata com o fato que muitos sistemas dinâmicos desobedecem a leis dinámicas para obedecerem a leis lineares que, na prática, tornam seu comportamento imprevisível. A teoria do caos tem relações estreitas com a geometria dos fractais, como o conjunto de Mandelbrot e de Mary, descoberto por Lorenz, conhecido pelo Lorenz Attractor.
Um importante campo na matemática aplicada é a estatística, que permite a descrição, análise e previsão de fenômenos aleatórios e é usada em todas as ciências. A análise numérica investiga os métodos para resolver numericamente e de forma eficiente vários problemas usando computadores e levando em conta os erros de arredondamento. A matemática discreta é o nome comum para estes campos da matemática úteis na ciência computacional.
[editar] Notação, linguagem e rigor
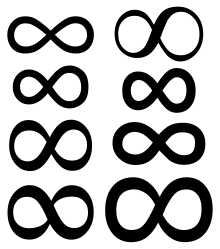
O símbolo do infinito ∞ em várias formas.
A língua matemática pode também ser difícil para os iniciantes. Palavras como ou e apenas têm significados muito mais precisos do que a fala do dia-a-dia. Além disso, palavras como aberto e campo têm recebido um significado matemático específico. O jargão matemático inclui termos técnicos como homeomorfismo e integral. Mas há uma razão para a notação especial e o jargão técnico : matemática requer mais precisão do que a fala do dia-a-dia. Matemáticos se referem a essa precisão da linguagem e lógica como "rigor".
[editar] Matemática como ciência
[editar] Conceitos e tópicos
[editar] Quantidades
Conforme o sistema de números foi sendo desenvolvido, os números inteiros foram considerados como um subconjunto dos números racionais (frações). Esses, por sua vez, estão contidos dentro dos números reais, que são usados para representar quantidades contínuas. Números reais são parte dos números complexos. Esses são os primeiros passos da hierarquia dos números que segue incluindo quaterniões e octoniões.
Considerações sobre os números naturais levaram aos números transfinitos, que formalizam o conceito de contar até o infinito. Outra área de estudo é o tamanho, que levou aos números cardinais e então a outro conceito de infinito : os números Aleph, que permitem uma comparação entre o tamanho de conjuntos infinitamente largos.
 | 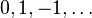 |  |  |  |
| Números naturais | Números inteiros | Números racionais | Números reais | Números complexos |
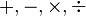 | π |  |  | |
| Aritmética | Constante matemática | Número ordinal | Número cardinal |
[editar] Estrutura
Muitos objetos matemáticos, tais como conjuntos de números e funções matemáticas, exibem uma estrutura interna. As propriedades estruturais desses objetos são investigadas através do estudo de grupos, anéis, corpos e outros sistemas abstratos, que são eles mesmos tais objetos. Este é o campo da álgebra abstrata. Um conceito importante é a noção de vetor, que se generaliza quando são estudados os espaço vetorial em álgebra linear. O estudo de vetores combina três das áreas fundamentais da matemática: quantidade, estrutura e espaço. |  |  |  | (()(()())) |
| Álgebra abstrata | Álgebra linear | Teoria da ordem | Teoria de grafos | Teoria dos operadores |
[editar] Espaço
 |  |  |  |  |
| Topologia | Geometria | Trigonometria | Geometria diferencial | Geometria fractal |
[editar] Transformações
Entender e descrever uma transformação é um tema comum na ciência natural e cálculo foi desenvolvido como uma poderosa ferramenta para investigar isso. Então as funções foram criadas, como um conceito central para descrever uma quantidade que muda com o passar do tempo. O rigoroso estudo dos números reais e funções reais são conhecidos como análise real, e a análise complexa a equivalente para os números complexos.A hipótese de Riemann, uma das mais fundamentais perguntas não respondidas da matemática, é baseada na análise complexa. Análise funcional se foca no espaço das funções. Uma das muitas aplicações da análise funcional é a Mecânica quântica. Muitos problemas levaram naturalmente a relações entre a quantidade e sua taxa de mudança, e esses problemas são estudados nas equações diferenciais. Muitos fenômenos da natureza podem ser descritos pelos sistemas dinâmicos; a teoria do caos descreve com precisão os modos com que muitos sistemas exibem um padrão imprevisível, porém ainda assim determinístico.
 |  |  |  |  |
| Cálculo | Cálculo vetorial | Equações diferenciais | Sistema dinâmico | Teoria do caos |
[editar] Fundações e métodos
Para clarificar as fundações da matemática, campos como a matemática lógica e a teoria dos conjuntos foram desenvolvidos, assim como a teoria das categorias que ainda está em desenvolvimento. |  |  | |
| Matemática lógica | Teoria dos conjuntos | Teoria das categorias |
[editar] Matemática discreta
Matemática discreta é o nome comum para o campo da matemática mais geralmente usado na teoria da computação. Isso inclui a computabilidade, complexidade computacional e teoria da informação. Computabilidade examina as limitações dos vários modelos teóricos do computador, incluindo o mais poderoso modelo conhecido - a máquina de Turing. |  |  |  |  |
| Teoria de números | Combinatória | Teoria da computação | Criptografia | Teoria de grafos |
[editar] Matemática aplicada
Matemática aplicada considera o uso de ferramentas abstratas de matemática para resolver problemas concretos na ciência, negócios e outras áreas. Um importante campo na matemática aplicada é a estatística, que usa a teoria das probabilidades como uma ferramenta e permite a descrição, análise e predição de fenômenos onde as chances tem um papel fundamental. Muitos estudos de experimentação, acompanhamento e observação requerem um uso de estatísticas.Análise numérica investiga métodos computacionais para resolver eficientemente uma grande variedade de problemas matemáticos que são tipicamente muito grandes para a capacidade numérica humana; isso inclui estudos de erro de arredondamento ou outras fontes de erros na computação.
 |  |  |  |
| Física matemática | Mecânica dos fluidos | Análise numérica | Otimização |
 |  |  |  |
| Teoria das probabilidades | Estatística | Matemática financeira | Teoria dos jogos |
[editar] Matemáticos notáveis
Referências
- ↑ An Old Mathematical Object (em inglês). The Mathematics Department of The State University of New York at Buffalo. Página visitada em 21 de dezembro de 2008.
- ↑ Earliest Uses of Various Mathematical Symbols (Contains many further references)
- ↑ NOVA ESCOLA. Direção e dimensão
[editar] Bibliografia
- BOYER, Carl B. História da matemática. 2ª Edição. São Paulo: Edgard Blücher Ltda, 1996. ISBN 8521200234.
- COURANT, Richard; ROBBINS, Herbert. O que é Matemática?. Ciência Moderna, 2000. ISBN 8573930217.
- DEVLIN, Keith. Matemática: a Ciência dos Padrões. Editora Porto, 2003. ISBN 9720451335.
[editar] Ver também
- Áreas da matemática
- Disciplinas que evoluíram a partir da matemática:
- Educação matemática
- Problemas em aberto da Matemática
- Olimpíadas
- Olimpíada Brasileira de Matemática
- Olimpíada Paulista de Matemática
- Olimpíada Brasileira de Matemática das Escolas Públicas
- Olimpíada Internacional de Matemática
- Prémios
- Prémio Abel
- Prémio Problemas do Milênio (Clay Math Prize)
- Medalha Fields
- Competições matemáticas
- Softwares
| Proprietários: | Livres: |
- Documentários

 Ver artigo principal:
Ver artigo principal: 



 Ver página anexa:
Ver página anexa: 



































Nenhum comentário:
Postar um comentário